分子物理学和热力学——《第七章》热力学的物理基础

本章内容在物理学中是相当独特的，也是初学者不太容易掌握的。关键在于我们研究问题的思想发生了微妙的变化。这种变化来源于我们对于物理过程的图象的不同。前面的力学以及分子运动的力学，还有后面的电磁学，对于物理过程的观察都是以相互作用作为基础的。也就是说，对于一个物理过程，我们总是从其中的相互作用力开始着手的。在获得了相互作用力的规律后，再寻求与这种相互作用力相对应的能量计算方法。因此在这种思路里，首先必须确定发生相互作用的对象，我们已经与几个这样的对象打过交道，例如质点，粒子，刚体，分子，还有我们后面要遇到的电子，原子，电磁场等等。

但在热力学中，却不是遵循这个思路，对于一个物理过程，我们并不考虑它的这种相互作用的机制，特别是对于涉及到物质状态的变化这种现象，其中的相互作用的机制并不是能够直接观察到的，而是往往需要我们事先构造一定的理论模型，例如前面的理想气体的分子运动模型。因此我们也可以纯粹从可以直接观察的反映物质状态的物理量出发，直接考虑其中的能量的变化与传递。

由于这样作并不是以物质的反映在具体结构里的相互作用力为基础的，因此有必要确定一些能量变化与转换的基本规律，从此出发，就可以定义用来刻划物质本身属性的物理量，而要进一步追寻这些物理量的物理根源，就需要考虑物质结构的内部相互作用了，但在热力学里，却不需要这么做，就好象我们每天吃饭，只是考虑吃得是否足够，而不用考虑吃进去的食物产生了那些作用。

只有习惯了这种思路，我们才有可能学好热力学，因此希望同学们多加体会。

功，热量，内能。

首先我们考虑如何计量一个物理过程中的能量变化。

一个宏观系统最明显的标志能量发生了变化的过程，就是作功。一个系统对外界作功或者是外界对系统作功，都是在系统与外界产生宏观的相互作用力时，所必然出现的情况。作功的测量与计算都是我们在力学里已经很熟悉了的。

第二种能量变化的方式就是传热了。传热本身是不需要作功的，经验告诉我们，只要让两个温度不同的物体接触，就会在这两个物体之间发生传热的过程，但传热有可能导致系统作功，总之使得系统的能量发生变化。

作用力作功与热量存在一个数值关系，这就是由焦耳通过实验得到的焦耳热功当量。

那么还存在什么过程，能使得系统的能量发生变化呢？这时只要暂时不涉及其它的能量形式，我们可以观察到，只要系统的初始状态和末状态给定后，无论中间过程是什么样的，这个期间的外界对系统所作的功，与外界向系统传递的热量的总和，或者反过来说，系统对外界所作的功与向外界传递的热量的总和，都是不变的。

因此在适当地规定系统与外界的作用形式的范围后，可以把系统与外界所能够发生的能量传递方式，看成只有作功与传热这两种方式。

那么既然传热和作功都使得系统的能量发生变化的同时，也就使得系统的状态发生变化，则我们还需要一个标志系统状态的能量的概念，这就是所谓系统的内能。

注意，从我们定义内能的方式可以看到，这个定义并不在乎究竟内能是表示什么样的运动的能量，也就是说，我们定义内能，并不需要一一地搞清楚内能由哪些种类的能量组成，然后再加起来得到总的内能，而是通过一种类似减法的思维方式来定义的，即系统状态发生了变化，处于末状态的系统的能量，减去外界对系统作的功，和外界对系统的传递的热量，剩下处于初始状态的系统的能量，要表征这种系统本身的能量状态，就自然地引入内能的概念。

热力学第一定律。

仔细的话，可以注意到，上面我们对内能的定义里隐含了一个假设，那就是系统末状态的能量减去作用过程中外界所加入的能量，就是系统初始状态的能量。这个假设是我们能定义内能的前提，并且不能由其它的物理学原理推导出来，而只能是我们从经验与实验中归纳出来的结论。这就是热力学的第一条定律：

外界对系统所传递的热量，一部分使得系统的内能增加，一部分使得系统对外界作功。

写出来就是

Q=E₂-E₁+A

由于能量是标量，因此我们应该注意这个表达式里的各个物理量的符号的约定。

热力学第一定律也可以表述为：第一类永动机是不可能的。所谓第一类永动机是指对外界作功后，又回到初始状态，同时不需要从外界获取任何形式的能量。

那么我们如何更为具体地分析热力学所描述的这么一个过程呢？这时，我们会发现一个隐藏的问题，那就是根据状态参量的定义，实际上我们无法描述系统从一个平衡态到另一个平衡态的转变过程中的系统状态，这样也就无从谈起考察系统从初始的平衡态到末平衡态的转变过程。而热力学第一定律所刻划的转变过程中的作功与传热又如何得到研究呢？

这时我们只有引入准静态过程的概念，在上章我们已经仔细讨论过。

引入准静态过程的概念后，我们就可以得到热力学第一定律的微分形式，也就是涉及平衡态的转变过程的形式：

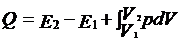
这个表达式表明作功与热量传递都是与系统的转变过程的具体路径有关。

热力学第一定律对理想气体等值过程的应用。

正如我们上面所分析的，应用热力学第一定律于具体的系统状态变化的前提，是尽量使得系统的不同平衡态之间的转变过程成为准静态过程，而在实验中，通过一定的方式，我们是能够作到这一点的。下面，就是遵循这样一个思路来分析理想气体的三个不同平衡状态之间转变的等值过程。

（一）等容过程。

顾名思义，等容过程就是系统的状态发生变化时，体积保持不变。要使得这个过程尽量趋向于准静态过程，可以使得外界的传热热源与系统的温度差总是保持很小，并且使得系统的状态变化很缓慢。

这样应用热力学第一定律矩可以得到：

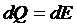
积分形式就是：

Q=E₂-E₁

即在等容过程中，外界传递给系统的热量全部转换为系统的内能，而系统没有对外界作功。

（二）等温过程。

顾名思义，等温过程就是系统的状态发生变化时，温度保持不变，而温度保持不变的意思就是系统的内能保持不变。要使得这个过程尽量趋向于准静态过程，可以使得系统与一个相对来说极大的恒温热库总是保持接触（因此可以假定另外的热源不能改变其温度），同时使得外界的作用于系统的压强无限缓慢地降低或增加，也就使得系统膨胀或压缩。

应用热力学第一定律可以直接得到：

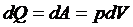
应用理想气体状态方程的积分形式就是：

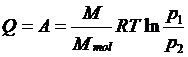
即在等温膨胀过程中，理想气体所吸收的热量全部转变为对外界作功；而在等温压缩过程中，外界对理想气体所作的功，全部转变为传递给外界恒温热库的热量。

（三）等压过程。

顾名思义，等压过程就是系统的状态发生变化时，压强保持不变。要使得这个过程尽量趋向于准静态过程，可以使得系统与一个极其缓慢增加温度的极大热库接触，并且保持系统所首都的外界压强不变。

应用热力学第一定律，对于理想气体来说就可以得到：

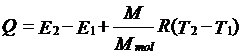
即在等压过程中系统所吸收的热量，一部分转变为系统的内能，一部分转变为对外界所作的功。

气体的摩尔热容。

用来刻划1mol的物质在温度升高1k时，所需要吸收的热量的物理量称为摩尔热容。

从上面我们对于等值过程的讨论可以知道，在不同的等值过程中，系统所吸收的热量转变为与温度对应的系统的内能的比例是不同的。

因此对于气体来说，我们分别有：

（一）定容摩尔热容。

根据对等容过程的分析以及气体内能的分子运动论定义，可以得到气体的定容摩尔热容为：

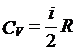
其中R为理想气体的摩尔气体常数。I为气体分子的自由度数目。

可以看到，理想气体的定容摩尔热容完全由气体分子的自由度决定。

（二）定压摩尔热容。

根据对等压过程的分析以及气体内能的分子运动论定义，可以得到气体的定压摩尔热容为：

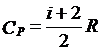
其中R为理想气体的摩尔气体常数。I为气体分子的自由度数目。

实际上，也就是：

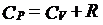
即理想气体的定压摩尔热容比定容摩尔热容大一个常数R。

而摩尔气体常数R因此也就可以解释为1mol理想气体在等压过程中，温度改变1k时，对外界所作的功。

同样可见，定压摩尔热容完全由气体分子的自由度决定。

还可以定义一个物理量，即定压摩尔热容与定容摩尔热容的比值，称为比热比。

绝热过程。

上面讨论的三种等值过程都必须与一个大热库相接触，下面我们考虑一个不与任何热库相接触的系统，也就是说，使得系统的外壁完全绝热。同样要使得系统所发生的任何过程是准静态过程，必须使得系统极其缓慢地发生变化。

既然对于绝热的系统不存在热量的变化，那么只有作功与内能之间的变化关系。而当气体由于体积发生变化而作功时，气体的内能也就发生变化，同时温度和压强都会发生变化，根据热力学第一定律和理想气体状态方程，可以得到绝热过程方程如下：

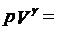
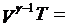
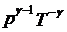
其中γ就是比热比。而这三个常数与气体的质量和初始状态有关，并且这三个常数互不相等。

循环过程。卡偌循环。

现在我们讨论一类极其重要的过程，就是系统经过任意的变化过程，然后回到初始状态，这意味着系统的初始状态与末状态相同，也就是说系统经过一系列变化，而我们不管这些变化是什么，内能最终没有发生改变。这就是循环过程。

循环过程之所以重要，是因为对于任何机器的工作，我们都要求是进行循环过程，也就是说，我们要求机器在开机前和关后的状态应该一样，而在循环过程中间，则要求机器完成我们所要求的任务。

最常用的机器就是所谓热机，即通过向机器输入热量，而机器把热量转换为对外界作功。实际热机的循环过程是相当复杂的，但在理论上，我们可以设计一些由我们上面所讨论的等值过程所组合成的循环过程，也就是说系统总是处于准静态过程，从而可以应用平衡态的热力学理论来分析循环过程的物理细节。

对于这种循环过程，我们讨论最经典的一种：卡偌循环。

卡偌循环是系统通过分别与两个恒温大热库交换热量而进行的循环过程，由两个等温过程和两个绝热过程组成，如下为理想气体的卡偌循环的压强-温度图：

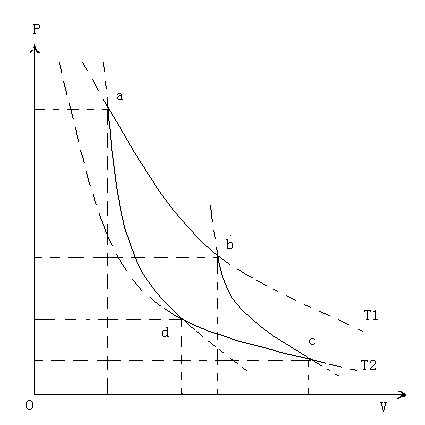
图中，ab与dc为等温过程，ad与bc为绝热过程。

我们考虑以a点为初始状态，按照abcda的顺序所作的循环过程：

（1）     作为一个循环过程，系统在过程中，分别与外界交换热量和作功。

（2）     气体对外界作功即abc所示的膨胀过程，大小由曲线abc下面的面积表示。

（3）     外界对气体作功即cda所示的压缩过程，大小由曲线cda下面的面积表示。

（4）     气体对外界所作的净功由闭合曲线abcd的面积表示。

（5）     气体在ab的等温膨胀过程中，从外界温度为T₁的高温热库吸收热量Q₁。

（6）     气体在cd的等温压缩过程中，向外界温度为T₂的低温热库释放热量Q₂。

（7）     根据等温过程的理想气体状态方程和绝热过程方程，存在关系：

。

（8）     卡偌热机的效率为：

。

可见效率与两个热库的温差有关，而且除非低温热库的温度为0k，热机的效率不可能达到100%。

同样可以考虑以a点为初始状态，按照adcba的顺序所作的循环过程，这就使得外界通过对系统作功，系统从低温热库吸收热量，从而使得低温热库降温，这就是所谓致冷机的原理过程。类似可以定义致冷系数：

。

热力学第二定律。

考虑上述卡偌热机的效率不能达到100%的缘故，是因为不可避免地需要向低温热库释放一定的热量，才能完成循环过程。从压强-体积图的几何方面来看，就是两根绝热线是不可能相交的，因此必须通过一个等温压缩过程回到与初始状态同一条绝热线上的状态上去，这同时就不可避免要释放一定的热量到低温热库。

开尔文通过总结这一类现象，得到一个一般的定律：

通过循环过程来工作的热机，不可能从单一热源吸收热量，然后把它转变为作功而同时不产生其他影响。

这就是所谓热力学第二定律的开尔文表述。

如果把从单一热库吸收热量并全部转变为作功的热机称为第二类永动机，那么热力学第二定律就是断言第二类永动机是不可能的。

换一个观点来看，就是热量通过热机转变为作功的过程是不可逆的。

热力学第二定律还有一种等价的说法，即所谓克劳修斯表述：

热量不可能自动地从低温物体传递到高温物体。

这同样可以理解为热量从高温物体向低温物体的传递是不可逆的。

实际上这两种不可逆性是等价的，而热力学第二定律正是刻划了所有的不可逆过程的共同特征。

可逆过程。不可逆过程

上面我们已经看到，热力学第二定律可以从一定过程的不可逆性这个角度来理解。那么在这个定律的制约下，就可以把一切过程也就分为可逆过程与不可逆过程两种。

实际上，只有理想情况下的没有摩擦的准静态过程是可逆过程，热力学第二定律最终断言了所有与热相关的宏观现象都是不可逆的。

卡偌定理。

对于完全由准静态过程组成的卡偌循环，反过来可以从热力学第二定律得到所谓卡偌定理：

（1）在温度为T₁的高温热源与温度为T₂的低温热源之间工作的一切可逆机的效率都是。

（2）在温度为T₁的高温热源与温度为T₂的低温热源之间工作的一切不可逆机的效率都不可能高于。

这条定理实际上给出了提高热机效率的途径，即提高两个热源的温度差。

热力学第二定律的统计意义和适用范围。

热力学第二定律刻划的是宏观热现象的不可逆性质，而宏观热现象完全是大量分子热运动的宏观统计表象，那么这种由热力学第二定律所表达的不可逆性质也必定是一种统计必然性。

实际上，这种由热力学第二定律所表达的不可逆性质表征了这样一种统计必然性：

对于一个不受外界影响的孤立系统，起内部发生的任何过程，总是从几率小的状态向几率大的状态进行，也就是说从包含微观状态数目少的宏观状态向包含微观状态数目多的宏观状态进行。

我们必须注意到热力学第二定律是针对一定的对象而言的，一方面这个对象系统必须是由足够大量的粒子组成，对于少数粒子组成的系统，甚至连用来刻划统计宏观性质的状态参量都用不上，更不用说热力学第二定律；另一方面，这个对象也不能大到包含整个宇宙，这超出了热力学第二定律的范围，因为我们是从一定有限空间里发生的过程中归纳出热力学第二定律的。没有理由保证我们把它推广到整个宇宙仍然是正确的，因为毕竟任何定律都还是基于对经验事实的归纳，而不是数学里的公理。

本文由奇点天文作者上传并发布，奇点天文仅提供文章投稿展示，文章仅代表作者个人观点，不代表奇点天文立场。