电磁波，它是否有一个“反震荡”

作者：伏远

摘要：将电磁波与已知几种物理学中重要的简谐震荡，如弦上的行波震荡，质点-弹簧系统震荡，L-C（电感-电容）电路的LC震荡，以及声波震荡等进行比较，由此提出一种假设，即，电磁波和上述几种简谐震荡一样，具有一个“反震荡”，它与电磁波的电场-磁场震荡相位相差π/2。

在一根沿x方向适当拉紧的弦上，在弦的一端沿Y方向施加一个力F，在理想无阻尼条件下，可以形成弦上的向X方向传播的行波，这个波可以用一个二阶偏微分波动方程描述，

式中M是弦的单位长度质量，即质量密度。
    （1）式的一个解是

y=y_mcos(kx-ωt) （2）^[1]

在0相位，y=y_m，弦上质点在Y方向位移最大，势能也最大；在π/2相位，y=0，此时刻弦上的质点在Y方向位移为0，处于平衡点，势能最小，速度及动能最大。

若（2）式描述弦上质点的位移变化，则

v=v_msin(kx-ωt) （3）

描述弦上质点的速度变化。在0相位，v=0，质点的速度及动能为0；在π/2相位，v=v_m，速度及动能最大，但质点位移为0，势能最小。（3）式与（2）式相差位相π/2。

若K代表系统动能，U代表系统势能，E代表系统总能量，则有

K=K_maxsin²ωt（4）

U=U_maxcos²ωt （5）

E= K_max=U_max。（6）

所以，这里存在着相互关联的两个简谐震荡，系统的能量在动能与势能之间来回传递，二者位相相差π/2。一个达到最大时，另一个达到最小，反之亦然，总能量守恒。

对于另一种情形的震荡，如一个理想无阻尼的质点-弹簧系统，也存在着类似的两个简谐震荡，质点的位移y和速度v可以分别表示为

y=y_mcos(kx-ωt) （7）

v=v_msin(kx-ωt)（8）

质点因速度产生的动能，因位移大小所具有的势能以及系统的总能量分别与（4）、（5）、（6）式相同。

对于一个包含电感L和电容C而理想无电阻的LC电路，可产生L-C震荡，并可用一个二阶微分方程来描述。可以证明，系统的总能量与E与储存在电感中的磁场能U_B以及储存在电容中的电场能U_E有如下关系，

U_B=U_B-maxsin²ωt（9）

U_E=U_E-maxcos²ωt （10）

E=U_B-maxx=U_E-max（11）^[2]

同样，这里存在着相互关联的储存在电感中的磁场能以及储存在电容中的电场两个简谐震荡，能量在磁场能与电场能之间来回传递。二者位相相差π/2，总能量守恒。

在这种L-C震荡中，电感器中的磁场和电容器中的电场，分别是“物理地”真实地建立起来的。

作为纵行波的声波，介质的质点在传播方向上的震荡位移y,为

y=y_mcos(kx-ωt) （12）

式中y_m是最大震荡位移值。

考虑声波传播中的介质质点遭受的压强变化，则有

p=p_msin(kx-ωt)（13）

式中P_m是压强最大值，p是瞬时压强。^[3]

声波所携带的能量，与介质质点的震荡位移和受到的压强的平方项成正比，并且在这两个量之间来回传递。同样地，这里的两个简谐震荡可以分别用正弦函数和余弦函数来表示，二者位相相差π/2，总能量守恒。

考虑电磁波。以下两式分别是由麦克斯韦方程组导出的在空间传播的电场E和磁场B的波动方程。

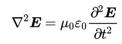
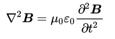
式中 μ₀和ε₀分别是真空磁导率和真空电容率。而

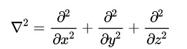
是拉普拉斯算子。

对于沿X方向传播的平面电磁波，上面两式可简化为

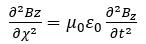
这两个分别关于电磁波的电场和磁场的二阶偏微分方程，形式和（1）式几乎完全相同。它们也可以有如下形式的正弦解，

E_y=E_maxsin(kx-ωt) （19）

B_z=B_maxsin(kx-ωt) （20）

这里电场在Y方向震荡，磁场在Z方向震荡，传播方向为X。^[4]

然而电磁波作为传播中的行波，其电场分量和磁场分量同步震荡，它们之间不存在相位差，必须同时刻达到最大或者最小。

以上列出的弦上行波震荡，质点-弹簧系统震荡，L-C电路中的LC震荡，以及作为行波的声波等，都可以用一个二阶微分方程来描述，都可以有正弦的或余弦的简谐解，可分析为相位相差π/2的两个震荡。或可以说，每个震荡都有它的一个“反震荡”，震荡的总能量在震荡和它的“反震荡”之间来回传递。

对于电磁波，同样可以用一个二阶微分方程来描述，（17）、（18）式与（1）式与有近似相同的形式，有正弦的或余弦的简谐解。但是因为电磁波的电场震荡和磁场震荡严格同步，相位差为0而不是π/2，电场震荡和磁场震荡不能互为“反震荡”。

比较（1）式和（17）、（18）式还会看到，系数因子M/F和μ₀ε₀处于二阶微分方程的相同的位置上。M/F=1/v²，v是弦上行波的波速；μ₀ε₀=1/c²，c是电磁波波速即光速。M/F中的M是弦介质的密度，表征了“介质的性质”；μ₀和ε₀分别是真空磁导率和真空电容率，表征了“真空的性质”。

电磁波所携带的能量用坡印廷矢量表示，

S=(1/μ₀) E_yx B_z（21）

这个矢量等于电场矢量与磁场矢量的叉乘。在电磁波的E_y与B_z同时为0的瞬间，矢量S等于0。

守恒和对称是物理世界的基本性质之一。在电磁波以光速传播过程中，既然在电场和磁场同时为0的那一点，代表能量的矢量S为0，那么，在这个时刻是否有另外一个“神秘的”未知物理量达到了它的最大值呢？这里我们建议一个假设，电磁波也许有一个未知的“反震荡”。

电磁波本身具有微观性质（光子），也具有宏观性质（电磁波谱）。与现代物理的广义相对论和量子力学相比，麦克斯韦等人建立起来的电磁波理论属于“经典”的和“老”的理论。然而，电磁波理论在今天仍然被用来解释很多实验现象。另一方面，迄今为止现代物理理论对电磁波的认识还远不能说已经彻底和完善，例如对波粒二象性等的理解。

参考文献：

[1] R.瑞斯尼克，D.哈里德.物理学 一卷二册 [M]. 北京：科学出版社，1980：（补充论题）A9-A11.

[2] D.哈里德，R.瑞斯尼克.物理学 二卷一册 [M]. 北京：科学出版社，1978：346-352.

[3] R.瑞斯尼克，D.哈里德.物理学 一卷二册 [M]. 北京：科学出版社，1980：640-642.

[4] D.哈里德，R.瑞斯尼克.物理学 二卷二册 [M]. 北京：科学出版社，1978：（补充论题）6-8.

本文由奇点天文作者上传并发布，奇点天文仅提供文章投稿展示，文章仅代表作者个人观点，不代表奇点天文立场。