《第三章》以太的性质与运动-以太的运动与密度分布

第三章 以太的运动与密度分布

按照天文学界目前流行的理论，暗物质是宇宙的主宰，但却不知道暗物质是什么。本文认为以太才是宇宙的主宰，星系只不过是以太海洋中的悬浮物体，但引领以太运动的却是星体。在本章中，以太的运动指的是宏观运动，是粒子的平均速度，如果类比空气，它就是“风”。

以太是宇宙的主角，星系的涡旋结构就是最好的证明。如图3-1所示，它与地球上的气旋结构相似：内核作刚体旋转，外层作较差旋转，中心具有喷流。如果没有以太，星系核是不可能作“刚体旋转”的，中心也不可能存在喷流，结构也不可能如此相似。

图 3-1. 地球上的气旋与涡旋星系的比较（图片来源于网络）

以太与空气类似，也具有一定的粘度，是以太粒子间的动量交换产生的。物体能够对其内部的以太部分拖曳，拖曳的程度与物体的折射率有关，物体的表面很难拖曳以太，因为以太的粘度系数小，也就是说，以太很难随着物体转动，但引力可以拖曳以太，以太可以跟随着大质量物体一起运动。

以太在宇宙中的运动包括拖动和转动，拖动是指在引力的作用下，以太跟随大质量物体的运动，而转动是指以太由于粘性而产生的运动。在宇宙中，以太很容易被拖动，例如，在太阳引力范围内（约1光年）的以太跟随着太阳一起绕银河系中心运动，但转动却较难，与太阳同步转动的以太在日冕（约1.3倍太阳半径）之内。地球对以太的拖动范围也很大，可达到金星和火星，但与地球同步转动的以太也只是在大气层内（约100千米）。

以太是流体，星体的质量越大，周围的以太密度就越高；星体的密度越高，以太的密度梯度就越大。星体周围的气体密度分布可表示为，其中，ρ₀表示星体表面的气体密度，G是引力常数，M是星体质量，m是气体粒子的质量，k是玻尔兹曼常数，T是气体的绝对温度，r₀是星体的半径，r是到球心的距离。以太也不例外，同样符合气体在引力作用下的密度分布规律。

3.1. 地月系

地月系是指由地球和月球构成的运动体系。

3.1.1. 密度分布

由于地球的质量较小，地球附近的以太密度可视为常量1.257×10^-6 kg/m³。

3.1.2. 速度分布

 在以太阳中心为参考系时，地球周围的以太基本上是与地球同步绕太阳旋转。但如果以地球中心为参考系，在大气层内，以太会与地球表面的速度同步。在大气层外，由于月球的拖动，以太绕地球中心旋转的速度随着距离的增加而增加，到月球轨道时达到最大，然后又随距离的增加而降低，估计达到150万千米（日-地系统的第二拉格朗日点）时，会出现逆转，而且逆转的速度越来越大，如图3-2所示。

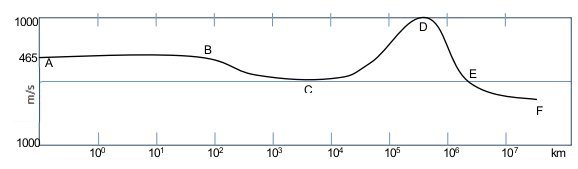
图 3-2. 地球中心为参考系时以太的速度分布（以地球表面为0点）

以地球的中心为参考系，以太的速度分布大概可分为5个部分，从A到B，以太与空气同步，绕球心转动，正是由于大气层内的以太与地球自转同步，才使迈克尔逊——莫雷实验出现零的结果。从B到C，地球对以太拖曳越来越弱，速度也逐渐下降。但从C到D，月球对以太的拖曳效果却越来越强，以太绕地球的速度逐渐变大，当高度达到月球轨道时，以太在月球引力的拖曳下，速度达到最高，从D到E，以太的速度逐渐降低，从E到F，以太开始逆转（逆转的原因有二：一是月球的质量有限，二是其他行星的影响）。

3.1.3. 地球周围以太运动的证据

1. 地球自转（0.465 km/s）的萨格纳克效应值可以测量出来（同步卫星进行中日双向时间传递实验），是以太与地球存在相对运动的最直接的证据，也是光速可变的最直接证据。假设中日双向时间传递实验所选择的卫星定点于北极上空，就不会存在萨格纳克效应。
2. 为什么公转30 km/s的萨格纳克效应值测量不到（中日双向时间传递实验，在任何时间所测量到的萨格纳克效应值都相等）？因为在地球中心参考系中，以太只有旋转运动而没有其他方向的运动（都随地球绕太阳运动）。
3. 国际空间站每年大约消耗7.5吨的燃料来维持轨道，说明空间站存在阻力，主流认为全部来至于地球大气的影响。我们知道：在空气中，直平面体风阻系数大约为1.0，球体风阻系数大约为0.5，但卫星轨道衰减的阻力系数却大于1.0，而且高度越高数值越大（马淑英等.大气阻力引起卫星轨道衰减的数值模拟[J]. 地球物理学报， 2013, 56(12): 3980-3987），如图3-3所示，图中四条曲线代表不同形状的卫星（图片是文中的插图）。

如果以太不存在，大气阻力系数是不可能随着高度的升高而变大的，因此，必定有一部分阻力是来自于以太，而且轨道越高，以太产生的阻力所占的比例越大。从图中还可以看出：大气与以太对物体运动的阻碍原理明显不同，大气对物体的阻力只与迎风面有关，但以太不仅与迎风面有关，还与物体的厚度及密度有关。

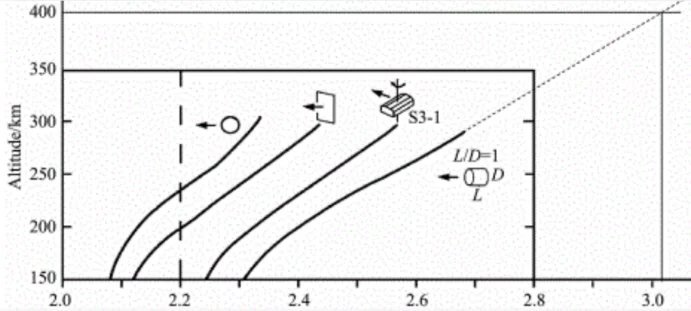
图 3-3. 大气阻力系数（横坐标）与轨道高度的关系

如果在空间站里做迈克尔逊——莫雷实验，就有可能测量出以太的运动方向。

3.2. 太阳系

在太阳系，以太并不需要以运动的方式来平衡太阳的引力（可以通过压强的变化），但在行星引力的拖曳下，以太也会绕太阳做圆周运动，因此，以太并不会阻碍行星的轨道运动（偏心率大的椭圆轨道除外）。

3.2.1. 以太的运动

由于行星引力的拖动，在黄道面上，以太与行星同步运行，也就是说，在水星以外，日球层顶以内，以太绕太阳的速度也基本符合的运行规律，如图3-4所示。

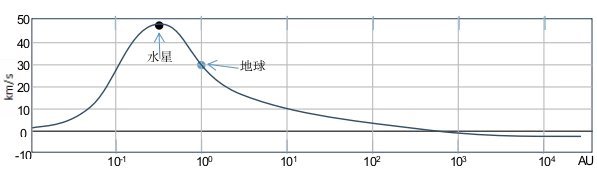
图 3-4. 太阳系中黄道面上以太的速度分布（以太阳表面为0点）

太阳周围的以太运动与地球周围的以太运动类似，在太阳表面，以太与太阳同步，但随着与太阳距离的增加，速度越来越高，到达水星轨道时，达到最大（与水星同步48 km/s），然后绕太阳的运行速度逐渐降低，估计超过800AU时，将会逆转。

3.2.2. 太阳系中以太运动的证据

A. 金星大气的环流运动

在金星的大气层顶，有从东到西的持续大气环流，只需要四个地球日就可以环绕金星一周，而且距表面越低速度越小，这种现象至今无人能够解释。如果承认以太的存在，引起这一现象的原因可能是地球和水星。由于地球的轨道速度比金星小，而水星的轨道速度比金星大，在水星和地球的拖动下，金星轨道内外的以太就会出现速度差，使金星周围的以太按顺时针旋转，如图3-5所示：

图 3-5. 金星周围以太的顺时针运动

金星周围以太的运动速度曲线如图3-6所示：

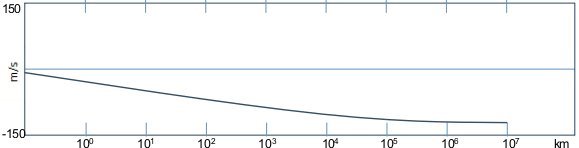
图 3-6. 金星中心为参考系时以太的速度分布（以金星表面为0点）

金星周围的以太涡旋是地球和水星的引力形成的，而金星的大气环流运动是以太拖动的。正是金星周围存在顺时针的以太涡旋，在以太的拖曳下，金星大气才会呈现出从东到西大气环流运动（这很可能也是金星倒转的原因）。

在其他的行星周围是否也有类似的以太涡旋呢？有，而且太阳系中的所有行星都存在！其证据就是逆行轨道。金星的逆行轨道只所以离主星如此之近，是因为它没有顺行卫星（如果有，金星大气就不会出现环流运动），如果水星有大气层，水星的大气也会象金星大气那样转动，如果地球外围没有月球的存在，地球上的大气也会象金星大气那样运动。

B. 逆行轨道

太阳系中所有气态行星外围的卫星几乎全部逆行，如木星系统中，轨道半径大于1800万公里的50多颗卫星只有一个例外（Valetudo，它是在2018年发现的在逆行区的顺行卫星，但这颗卫星不可能在逆行区内长期存在），其原因还是由于主星轨道内外的以太速度差而形成的以太涡旋，木星周围以太的运动速度曲线如图3-7所示：

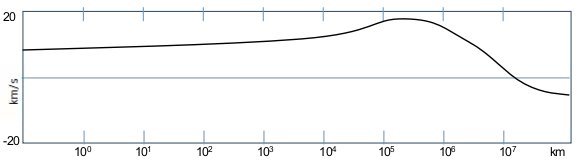
图 3-7. 木星中心为参考系时以太的速度分布（以木星表面为0点）

木星周围的以太，与木星中心的相对静止点大约在1500万公里处，在1300—1700万公里范围内没有任何卫星存在。木卫四十六是一个例外，它是顺行卫星中最远离木星的一颗，但这颗卫星的轨道也会在以太的阻力下，其轨道半径将逐渐下降，直到以太顺行区，也就是说，在外围的顺行卫星不能长时间存在。

为什么卫星总是以群居的方式存在？例如，亚南克卫星群、加尔尼卫星群等，这是因为质量大的星体能够影响以太的运动，但以太却能够影响小质量的星体运行，小质量星体只有与以太运行同步，它才能够保持轨道的稳定。

C. 太阳系最强的风暴 

海王星处于太阳系的外围，行星离太阳越远，驱动风暴的能量就越少，但海王星上却存在太阳系中最强的风暴，测量到的风速高达2400km/h，而且风向与海王星的自转方向相反，其原因就是海卫一的逆行，它对以太的拖动能力比海王星表面对以太的转动能力大，从而引起海王星周围的以太反转。如果这样的情况继续下去，海王星的自转周期将有较快的上升。海王星周围的以太速度如图3-8所示：

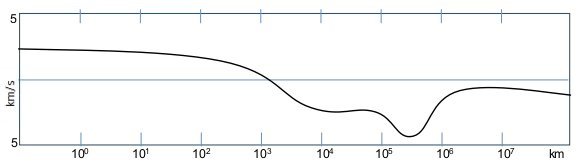
图 3-8. 海王星中心为参考系时以太的速度分布（以海王星表面为0点）

与其他大型卫星不同，海卫一运行于逆行轨道，它是被海王星近期俘获的，由于它占围绕海王星公转的所有质量的99.5％（包括海王星环和其他13个已知的卫星），因此，对海王星的运行造成了极大的影响：它的顺行卫星将会逐渐消失（轨道逐渐降低，最后坠入海王星），而且它的自转速度也会加速变慢。

D. 较差自转 

拥有顺行卫星的星体，其赤道的自转角速度大于两极，例如：太阳（赤道附近每25天转一圈，极区37天转一圈）、木星（赤道9小时50分钟，极区9小时55分钟）、土星、天王星等。但拥有逆行卫星的星体则相反，例如：海王星的赤道自转周期约为18小时，在两极只有12小时。海王星的较差自转是太阳系中最明显的，还是因为海卫一的逆行，星体自身结构内部的对流并不能解释较差自转。

可见，在太阳系中，总体上是以太跟随着行星运动，但每个行星周围的以太都存在一个逆行轨道，在太阳系的外围，以太同样存在逆行轨道，逆行的慧星就是最好的证明。以太的运动规律是：大质量天体拖曳以太，但以太能影响小质量天体（也包括微观粒子）的运行。

3.2.3. 以太与太阳风

A. 太阳风的产生

在帕克的理论模型里，太阳外层的日冕温度极高，达到百万度的数量级。这样的高温会产生完全电离的等离子体。因为温度太高，这些离子的动能很大，大到可以冲破太阳的引力束缚飞向地球。而且，帕克用详细的理论推导表明，从日冕中释放出来的离子最后会突破音速临界点被加速至超音速。对于这种从太阳向外释放的离子流，帕克称之为“太阳风”。

今天的科学家们已经知道：帕克的热驱动风模型并不能解释持续不断的高速太阳风，高速太阳风并不像帕克认为的那样是从高温的日冕中流出的，恰恰相反，它是从温度较低的冕洞中产生的。在极紫外光和软X射线太阳图像中，冕洞显示为日冕的黑暗区域，它们看起来很暗因为它们是比周围等离子体更冷、密度更小的区域，而且磁力线是开放的。这种开放的磁力线结构使太阳风更容易逃逸到空间，导致相对快速的太阳风流。因此，人们普遍认为磁场对于产生持续高速的太阳风有着特殊重要作用，但磁场是如何对太阳风产生影响的？磁场是从哪里来的？谁也说不清楚。

本文对太阳风的产生有如下观点：

涡旋与喷流在太阳大气中无处不在，在活动区、宁静区以及冕洞区域都能观测到涡旋与喷流的存在，并在各个太阳大气层中均能观测到，例如色球喷流及日冕喷流等。

太阳风最初是在色球中产生的，色球中的针状物就是太阳风的起点。在色球中，可以发现太阳的边缘有很多毛刺状的喷流（即针状物），这些针状物间歇性地以约25公里每秒的速度从色球层喷出到日冕中，从而完成对太阳风的第一次加速。

日冕中也同样存在喷流，与色球中的喷流（与地球大气层中的飓风类似）具有相似的原理。但日冕中的喷流与色球中不同，它与地球上的龙卷风具有相似的结构：纤细的丝状物，长长的环状物以及类似指纹一样的螺纹在整个日冕中起舞。阿尔夫文的理论也认为，日冕中存在“太阳磁通管”（俗称为太阳上的“小喷泉” ），本文认为：所谓的“太阳磁通管”应该就是以太为主体的涡旋，这就是太阳风的第二次加速。

地球上也存在飓风，但为什么它不能把空气分子抛出大气层呢？我们知道：地球上的飓风一般不超过3万米的高度，这是因为高空的空气密度小。但太阳日冕外层的大气密度也不大（约为10^-12 kg/m³，），它是如何把质子和电子抛出去的呢？这就必须依靠以太的帮助，如果以太不存在，这种加速机制只会存在于色球和日冕的底层中。在日冕底层中的质子密度与以太的密度（1.26×10^-6 kg/m³）相当，因此，喷流可以在日冕层中一直存在。如果把日冕中的喷流与地球上的水龙卷作比较：质子的作用相当于水蒸汽，以太相当于空气，质子向上加速过程是螺旋式的，与地球上水龙卷中水分子的上升路径相似。

可见，太阳风的形成是涡旋与喷流的产物，属于自加速，但能量来源于光球。在色球层中，涡旋以激态的氢原子为主，色球层中的针状物就是激发态的氢原子向上加速所表现出来的现象。在日冕层，涡旋以以太为主，美国宇航局的界面区域成像光谱仪（IRIS）所拍摄的纳米喷气流应该就是这种涡旋，这种涡旋只存在于以太密度大于太阳大气密度的区域。

太阳风在加速过程中，对质子和电子的加速几乎是一样的，因此，电子的温度要比质子低一千多倍。高速太阳风主要来自两极的原因，应该是由于磁场的开放，但更直接的原因可能是：极区附近带有相同的净电荷。

• 太阳风的切向速度

现代观测已经证明，地球附近太阳风的前进方向总是垂直于地球运动的方向，也就是说，太阳风的横向速度与地球的轨道速度相等（地球的弓形激波为证）。

从彗星的离子尾也可以看出：太阳风的切向速度总是与彗星垂直于太阳的轨道速度分量相等（因为离子尾是太阳风造成的，而且它总是在太阳和彗星的连线上），如图3-9所示。如果彗星的轨道是圆形的，太阳风的切向速度必定与彗星的轨道速度相等（小于水星轨道的彗星除外）。

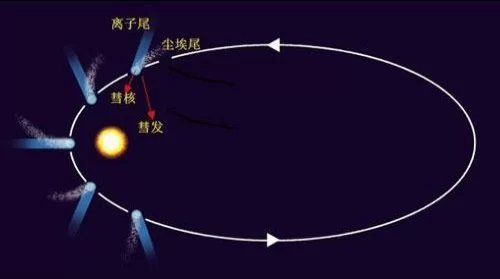
图 3-9. 彗星的离子尾（图片来源于网络）

帕克太阳探测器的升空，更是证明了太阳风受到以太横向运动的影响：在第一次靠近太阳期间，帕克在距离太阳36倍太阳半径的地方，测出了每秒大约30~50千米的切向速度，而根据此前的模型，太阳风的切向速度应该最高只有每秒4千米，是理论预测值的10倍。如果没有以太，太阳风的横向速度是无法解释的。可以预测：随着帕克逐渐靠近太阳，太阳风的横向速度将会越来越小。

因此，可以认为：太阳风切向速度产生的原因是由于以太跟随大质量物体的运动，太阳风中的质子和电子在以太流体的影响下，其切速度会与以太绕太阳的速度相差不多。

• 太阳风的径向运动

当太阳风离开太阳后，在切向上，跟随着以太运动，与以太的切向速度保持一致（因为以太的密度比太阳风的密度大很多倍），但在径向上，受两种力量的控制：一是以太的阻力（包括太阳的引力），二是光压产生的推力（彗星的尘埃尾可以证明）。太阳风的速度是两种力量较量的结果，当光功率密度较大时，质子的温度下降较慢（或不降），但电子的温度却不降反升。如果失去了光压的推动，太阳风在以太的作用下，会在太阳的边界会产生阻尼振荡，径向速度终将下降为0。旅行者1号是2012年、旅行者2号是2018年被宣布离开太阳系的，它40多年间飞行了200多亿公里，2019年科学家重新分析了旅行者2号在太阳系的边缘传回的数据，发现了旅行者2号在这个地方的飞行明显受阻。

太阳风在太阳附近会出现天文学家称之为“回折”的现象，这种现象应该是以太的涡旋引起的，与磁场无关。太阳周围的以太在水星引力的牵引下，切向速度会大幅升高，但以太是流体，必然会产生一个个的涡旋。

D. 日珥的运动

日珥也是产生太阳风的原因之一，日珥的运动很复杂，具有许多特征。日珥不断地向上抛射或落下时，若干个节点的运动轨迹往往是一致的。当日珥离开太阳表面时，速度会不断增加，这种加速是突发式的，属于涡旋加速，在两次加速之间速度基本保持不变。日珥的密度远大于日冕，但宁静日珥可长期存在于日冕中，既不坠落也不瓦解，是什么力量支撑和维持著它？活动日珥和爆发日珥的速度可高达每秒几百公里，动力从何而来？日珥运动往往突然加速，甚至宁静日珥会一下子转变为活动日珥，原因是什么？

日珥实际上就是色球层中的巨形针状体，与其他的针状体其形成的原理是相同的，都是一种涡旋，因此，当日珥离开太阳运动时，速度才会不断增加。日珥一般也分为两次加速，第一次加速在色球层，以激发态氢原子为主导，第二次加速在日冕层，以以太为主导。

日珥是在色球层中形成的，它的成分与色球基本相同，对于上升到日冕中的日珥，其密度与以太的密度应该相差不多，因此，当日珥物质升到一定高度后，会慢慢地降落到日面上，有些既不坠落，也不瓦解，其原因可能有三：一是涡旋的原因，二是以太与日珥的密度差异不大，三是所带的净电荷与太阳表面相同（如果日珥中所带的净电荷与太阳表面相反，它就会加速下落，其运动的轨迹与拱型门相似）。

3.2.4. 太阳系中的暗物质

万有引力定律是正确的，但前提条件是：以太的分布必须是均匀的（因为以太粒子也有质量）。但在引力的作用下，以太的分布并不均匀，可表示为：，因此，万有引力定律中的中心天体质量M就必须修正，需要包括由于以太密度分布不均所引起的附加质量，如果不考虑以太的运动，可表示为，其中L为到中心天体的距离，修正后的公式为。从上面的分析可以看出：在天文学中所谓的“暗物质”，指的是由于以太密度分布不均所引起的附加质量，是引力所产生的“效应”。

下面计算以地球为观察点，地球轨道内的暗物质质量：

以太阳中心为原点，地球轨道的长度L为半径作一球体。由于对称球壳对球壳内物体的万有引力作用的合力为零，对于距离大于L的部分，可以看成许许多多同心球壳叠加而成，因此，对于球体外围的以太，可以看成对地球没有万有引力作用。

在太阳周围，如果不考虑以太的运动，设以太的密度系数，其中M为太阳的质量，m为以太粒子的质量，R为太阳的半径。则以太的密度可表示为，由于A= 3.57×10^-6（忽略以太的温度变化，因为以太只是能量传播的介质，吸收能量很少）远小于1，上式可简化为：。在地球轨道内，暗物质质量为= 1.47×10²⁰ kg，相当于地球质量的40000分之一，而地球轨道内以太的总质量为= 1.78×10²⁸ kg，这就是太阳系中观察不到“暗物质”的原因，但太阳系中以太的绝对质量（每立方光年为5300亿倍太阳质量）比太阳质量大很多倍。

3.2.5. 水星轨道的进动

影响水星轨道有很多的因素，主要包括：

1. 太阳

太阳对水星轨道的影响主要包括三个因素，第一是太阳大气的阻力；第二是太阳风粒子（太阳一直在向外发射高能粒子）；第三是不完美的重力场，太阳不是一个点质量，而是一个有着不规则重力场的球体，这个不规则的重力场作用在水星上，就导致了潮汐力，水星运行到距太阳越近，受到的潮汐力越大。

• 行星

在太阳系中，除水星外，还有其他的七大行星，特别是金星、地球和木星能对水星的轨道产生一定的影响。但其他的行星只影响水星的轨道周期，对轨道的进动影响很小，因为其他行星是随机分布的，其他行星只能引起水星角速度的减少，而不会使水星正向进动，因此，有人用设想的一个更靠近太阳的行星（被称为火神星）来解释。水星处于最内层，金星、地球、木星等都在水星的轨道之外，它们对水星的摄动只能引起角速度的减少，也可能会有少量的负向进动，但不会有正向进动，中国科学院地质与地球物理研究所的汤克云研究员在《金星对水星的摄动肯定为负》中说明了原因，并计算出金星等七大行星所引起的水星轨道进动约为每百年负600角秒。 

• 以太

水星每百年有574.6角秒（除去岁差）的正向进动，很可能是以太起主导作用。以太对水星的运动影响主要有两个方面：

一是由于太阳的引力引起的以太密度分布变化，也就是暗物质的作用。水星的运行轨道是椭圆，距离从 4600 万公里到 7000 万公里变化。可以计算出：距太阳4600 万公里时，轨道内的暗物质质量约为= 1.38×10¹⁹ kg，距太阳7000 万公里时，轨道内的暗物质质量约为= 3.19×10¹⁹ kg。也就是说，水星绕太阳运行时，水星所感受到的太阳质量不是恒定的，其变化值为∆M= 1.81×10¹⁹ kg，这是水星正向进动的原因之一，但这个值太小，不是主要原因。

二是以太的阻力。由于水星的运动是椭圆，也就是存在切向运动和径向运动，但水星的径向运动不能有效引导以太绕太阳运动，这必然会导致水星与以太的运动不同步，在近日点水星的速度比以太的速度大。在以太的阻碍下，水星会出现轨道衰减，也就是说，水星运动到近日点时，在以太和太阳大气的阻碍下向太阳靠近，从而导致近日点的距离减小。其结果就是水星的离心率增加、轨道周期减少，这才是水星进动的主要原因，进动量与相对以太的速度有关，但这种阻力所引起的进动很难计算，本人没有计算能力。

水星的运动轨迹实际上是水星向太阳的旋进，其轨道角动量会逐渐减少，主要原因就是以太的阻碍。这种例子在宇宙中很常见，当一个双星系统距离很近时，随着互绕速度的增加，以太的阻碍作用也会越来越明显，最后发生碰撞，这就是轨道衰减。对于近地轨道卫星，由于卫星相对以太和地球大气的速度高，同样存在近地点的进动和轨道衰减，因此，必须定期提升卫星轨道的高度。需要指出的是：地球大气与以太都会阻碍卫星的运动，但阻碍的方式却不同，大气阻碍可以比喻成潜艇在水中航行，必须把水分子推开，而以太阻碍可以比喻成球形的钢网在水中运动。

3.3. 银河系

在银河系，由于以太密度的分布不均所引起的“效应”就非常明显。在银核，以太的密度大，但随着距离的增加，其密度逐渐减少。在距银核同样的距离上，银道面上（尤其是旋臂上）的以太密度比其他地方高。在与银核相同的距离上，恒星所处位置的以太密度越高，其轨道速度就越低，反之则越高。在很多星系中，由于以太密度变化引起的附加质量成为维系星系的主要力量。

银河系中实际物质密度的分布相当复杂，以太与可见物质混合在一起，由于以太的质量远大于可见物质的质量，例如：在太阳系附近，可见物质的密度约为每立方光年0.004个太阳质量，也就是9.45×10^-21 kg/m³，比以太的密度1.257×10^-6 kg/m³小很多倍，因此，可以把可见物质的密度纳入到以太的密度之中。

假设银河系中心黑洞也是由以太粒子组成的，它就与气态行星一样，没有明显的表面，估计固体半径约1000公里，在外层，以太气体的密度变化同样遵循，由于无法得知黑洞表面的以太温度，它附近的以太密度分布无法计算。但当r > 1光年时，可以认为以太的温度不再变化。

3.3.1. 以太的密度与速度

为了便于说明，把银河系分为三个部分，r < 1光年，称为核心，1< r< 1000光年，称为内层，r>1000光年，称为外层。

A. 在核心，由于黑洞质量一家独大，恒星的运动速度基本符合开普勒三大定律，以太密度的变化对恒星速度的影响可忽略，也就是说以太的影响很小，与太阳系相似。

B. 在内层，恒星的速度可以看成黑洞与附加质量引起的速度迭加：，如图3-10所示，图中用红色曲线表示的是银盘中恒星运动的实际速度曲线（通过观测得出的结论），它可拟合为黑洞质量引起的恒星速度m/s（蓝线表示）和附加质量引起的恒星速度m/s（绿线表示）的叠加，其中r表示到黑洞的距离，单位是米。

由于，m/s，可得出内层中的附加质量与距离的关系：。其原因是：以太的密度分布近似球形，而附加质量可表示为：，因此，内层中的以太密度可表示为，其中，r的单位是米，常数B = 4.39×10¹⁵ 。

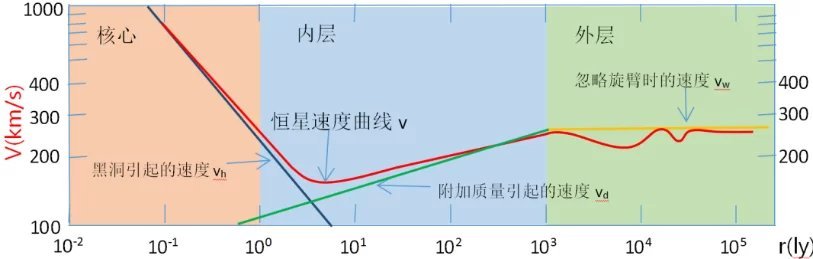
图 3-10. 银盘中恒星的速度曲线

C. 在外层，由于银盘的存在，以太的等密度曲线不再是球形，可以等效为厚度为h的圆盘，附加质量可表示为：，因此，以太的密度与距离的关系可表示为：，附加质量与距离的关系也可表示为：，其中，D和k都是常数，由于，因此，以太的速度是与距离无关的常量。这种计算方法在数学上是不严谨的，但本文的目的是原理的说明。在外层中，恒星的速度的变化主要是旋臂造成的，因为旋臂中的物质密度高，产生的附加质量小，恒星的轨道速度慢。如图中黄线所示（没考虑旋臂的影响）。

从上面的计算可以看出：当r > 1光年时，银河系中以太的密度变化很小，因此，可以认为常数C= 1.257×10^-6 kg/m³，它的大小对计算没有影响。

3.3.2. 旋臂的产生

 1964年﹐美籍科学家林家翘建立了密度波理论，该理论认为﹐恒星在绕中心旋转时﹐绕转的速度和空间密度都是波动变化的。运动慢则恒星密集﹐反之则稀疏﹐因而空间密度也呈现波动变化，这种波被称为密度波。这种波既绕中心环行传播﹐同时又沿半径方向传播﹐因而密度极大的波峰呈旋涡状分布﹐从而形成旋臂。恒星进入旋臂后因为恒星密集和引力场加强而减慢速度﹔反过来﹐速度减慢使恒星“拥挤”一起﹐密度增大﹐引力场加强﹐因而使这种状况得以自行维持。

但是，恒星一旦进入旋臂引力势阱后，还能运动出来吗？

我们知道，在任何旋转的流体中，流体的表面都会形成波浪，也就是说，介质质点的速度总有一定的差别，也会存在密度上的差异。当星体附近的以太密度较高时，它所受到的附加质量的引力小（附加质量的大小与本地以太的密度有关），绕行的速度就会慢，速度的变慢，就会导致星体的聚集，从而导致旋臂的形成（与道路上的车流是同样的道理，车流的密度只与道路有关，而与车辆无关），它实际上是以太密度对星体速度的反作用。旋涡结构是由星体的运动产生的，但旋臂并不是永远由同一批星体组成。也就是说，旋臂由以太的密度波构成的（地球上的气旋也存在旋臂结构），它并不与星体相联，星体的角速度是可变的。正是这种运动维持了旋涡星系的结构。恒星进入旋臂后，由于引力的减少，速度会降低，当以太的密度减少时，星体将恢复它的轨道速度，以太密度波的旋转速度应比星体的旋转速度稍慢。

如果以太不存在，就没有密度波，旋臂也就无法形成。以太跟随星体运动，但以太对星体的运动也存在反作用。

3.3.3. 涡旋与喷流

在流体中，喷流是指流体沿着涡旋垂直方向的运动（例如气旋中心的向上运动），涡旋能产生喷流，喷流也能产生涡旋（气旋就是气体的向上运动产生的），二者是伴生关系。

涡旋产生喷流的必要条件是：核心是刚体旋转。当流体刚体旋转时，刚体边缘的转速最大，压强最低，外面的流体向内流动，但又无法到达中心，只有转向，从而形成喷流，飓风的喷流就是在风墙处。银河系也存在喷流，喷流的位置大概在1000光年处，那里是刚体旋转的边缘，如图3-11所示。

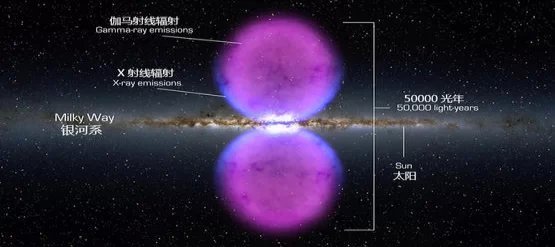
图 3-11. 银河系的喷流（图片来源于网络）

图中的X射线和伽马射线是粒子在以太中运动时产生的，其频率与粒子的速度（相对于以太）有关：。例如，如果质子在喷流中相对以太的的速度达到500 km/s，它所产生的辐射频率为6.3×10¹⁷ Hz，在X射线的频率范围内。

不过，主流天文学家认为银河系的喷流是大约在200至400万年前人马座A^*发生了一次超级爆发，剧烈的喷发在银河系中心两侧形成了一对巨大的气泡状结构，直到现在气泡结构依然还在向外扩散。但是，是什么爆发能够爆发出如此规则的形状？

3.3.4. 吸积盘与喷流

在高密度星体周围的涡旋，我们通常称之为吸积盘。吸积盘通常是一种由弥散物质组成的、围绕中心体转动的结构。如果中心天体的角动量较小，盘内的摩擦力将使气体逐渐螺旋下落，被吸积到星体。传统认为：重力使得盘中的物质沿螺线被吸附至中心体，角速度的不同则使得物质进行着角差转动，而引力场使得物质被压缩，同时激发出电磁辐射。

但是，引力场是如何压缩物质的？又是如何激发电磁辐射的？质量和能量又是如何转化的？中子星及黑洞产生的吸积盘辐射多半处于光谱的X-射线区域，但分子气体的发光不可能是热致发光，因为分子气体不可能有如此之高的温度（否则，气体四散，无法形成吸积盘）。围绕在星体周围旋转的分子气体，虽然速度较大，但其相邻气团的速度相差却很小，雷诺系数不可能很大（我们所观察到的吸积盘，雷诺系数都很小），气体间的摩擦也不可能使温度升高到发射X射线，吸积盘中的能量转化效率更不可能比核聚变还高出10多倍。

关于喷流的产生，最广为接受的是从中心黑洞抽取能量的理论。罗杰·布兰福德和罗马·日纳杰于1977年提出：吸积盘附近的磁场被自转的黑洞拖拽，当磁力线聚集起来时，相对论性粒子加速后被发射出去。彭罗斯理论认为，从中心黑洞抽取能量依靠的是广义相对论中的参考系拖拽效应。

但是，目前为止，我们连磁场是什么都说不清楚，而且吸积盘是电中性的，如何与磁场产生作用？磁场又是如何被自转的黑洞拖拽？磁力线又是如何聚集起来的？又是如何发射粒子的？

一般高密度、快速旋转的星体都会出现喷流，最可能的过程是：由于以太的粘度随着密度的升高而增加，大密度星体周围的以太会随着星体作刚性旋转。在吸积盘上，分子气体在引力的作用下会螺旋下降（因为分子气体的速度比以太的高），但当分子气体下降到以太刚体旋转的边缘时，气体分子就不会继续下降，只能沿着旋转轴向外喷发（因为分子气体的速度比以太的低）。喷流需要消耗涡旋的能量，也就是会降低涡旋的速度。如果星体的角速度较小，可以从周围吸收物质增加角动量，但角动增加到一定程度时，会产生喷流，吸收物质的能力也会下降，这也是喷流具有周期性的原因。

在高密度星体的周围，以太的密度较大，因而粘度也较大，星体的表面完全能拖曳它，使它与星体同步旋转。分子气体的辐射是由于气体分子相对以太的运动速度引起的，气体分子辐射的频率为，其中v是分子相对于以太的速度。在吸积盘中，分子气体与以太运动速度不同，二者的速度曲线如图3-12所示（图中红色代表分子气体，蓝色代表以太，当以太的速度大于气体分子的速度处，分子气体会产生喷流）。银河系的中心天体也存在喷流，如图3-13所示。

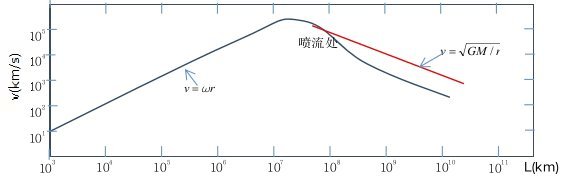
图3-12.银河系中心吸积盘与喷流的形成

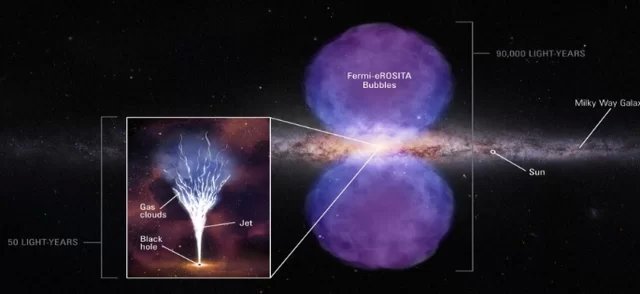
图 3-13. 银河系中心喷流（图片来源于网络）

3.3.5. 以太密度在银河系的分布规律

A. 核球

核球是指银河系的中心天体，也就是天文学中的人马座A*（sgr A*），俗称为“黑洞”。假设它也是由以太粒子组成的，没有经历恒星过程，是直接由以太气体坍缩成的超大质量黑洞，结构类似于气态行星，它没有明显的固体表面，其密度分布类似单边高斯分布，如图3-14所示：

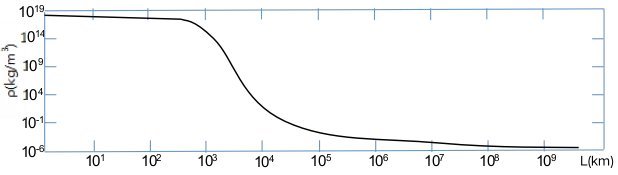
图3-14. 核球的密度分布

在黑洞的中心，以太的密度（2×10¹⁸ kg/m³量级）和压强都很高。由于黑洞内部的温度是气体压缩引起的，没有热源，因此，它的表面温度并不高，是一个不发光的球体。假如黑洞质量为4百万太阳质量，可以认为黑洞核心部分是一个密度为2×10¹⁸ kg/m³，半径为1000公里的球体，呈固体状，从1千公里到10万公里，是从固态到气态的过渡层，10万公里外可以认为是黑洞的大气层。

B. 银心

这里指距银核大于1光年，小于1000光年的球体，如果不考虑以太的速度，以太的密度分布近似球形。以太密度可表示为，其中，C= 1.257×10^-6 kg/m³，r的单位是光年。

C. 银盘

这里指距银核大于1000光年的银道面，如果不考虑以太的速度，以太的密度分布与距离的关系近似线性，可近似表示为，其中，r的单位是光年。

令，可拟合银河系中银道面上的以太密度曲线，如图3-15所示，当距银核大于1光年时，银河系中的以太平均密度变化幅度不会超过10^-12 kg/m³。

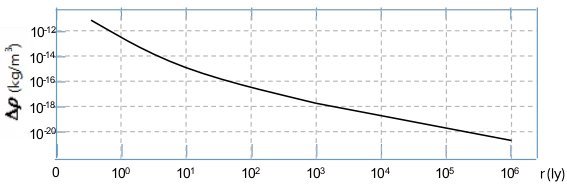
图3-15. 银河系中以太的密度与距离的关系

本文由奇点天文作者上传并发布，奇点天文仅提供文章投稿展示，文章仅代表作者个人观点，不代表奇点天文立场。