第二章 以太的物理性质

假设以太是由以太粒子（密度量级为2×1018 kg/m3的球状物）组成的，并以气体的方式存在于宇宙之中，具有理想气体的所有性质（粒子间没有相互吸引与排斥，粒子之间的碰撞为完全弹性碰撞）。由于技术的限制，我们还无法直接对以太进行测量，只能假设以太是电磁波传播的介质，并根据电磁波的性质进行推测。

2.1. 以太的密度

在现代电磁学中，认为以太不存在，电磁波是电场与磁场在真空中的互激，并自持传播，是运动的电磁场。因此，电磁波中电场为涡旋电场，其强度为E，磁场也是涡旋状，强度为H。在声学中，由于空气是声音的传播介质，因此，定义大气压受到声波扰动后产生的变化量为声压p，空气体积元速度为u。

2.1.1. 声波与电磁波的比较

A、波阻抗

声波的阻抗定义为：，电磁波的阻抗定义为：，由于声波阻抗也等于介质密度与传播速度的积：，真空中电磁波的阻抗也可表示为：（为真空磁导率），因此，，。

• 平均能量密度

声波的平均能量密度可表示为，声波的能量包括动能和位能，各点的动能与位能相位相同，大小相等，也就是说，动能达到最大值时，位能也达到最大值，总能量也达到最大。能量不是储存在系统中，而是具有传递特性，这是自由行波的一个特征。

电磁波的平均能量密度可表示为（ɛ₀是真空介电常数），与声波一样，电磁波的能量包括电场能量和磁场能量，各点的电场能量与磁场能量相位相同，大小相等，当电场能量达到最大时，磁场能量也达到最大，总能量也达到最大，也具有自由行波的传递特征。

• 平均能流密度

平均能流密度是能流密度（单位面积的能量传输速率）在一个周期内的平均值。声波的平均能流密度可表示为：，电磁波的平均能流密度是用坡印亭矢量表示的：，虽然二者的表达式不完全相同（原因是声波是纵波，而电磁波具有横波特征），但所得到的数值却是相同的，量纲也相同。

• 辐射压力

声音与电磁波都存在辐射压力，而且计算方法也一样，其数值都等于平均能量密度，其量纲也相同：焦耳/米³  = 牛顿/米²。例如，声压级为100dB的声波，其声压为2 Pa，已知空气的密度为1.29 kg/m³，速度为332 m/s，就可以求出声音的平均能量密度为

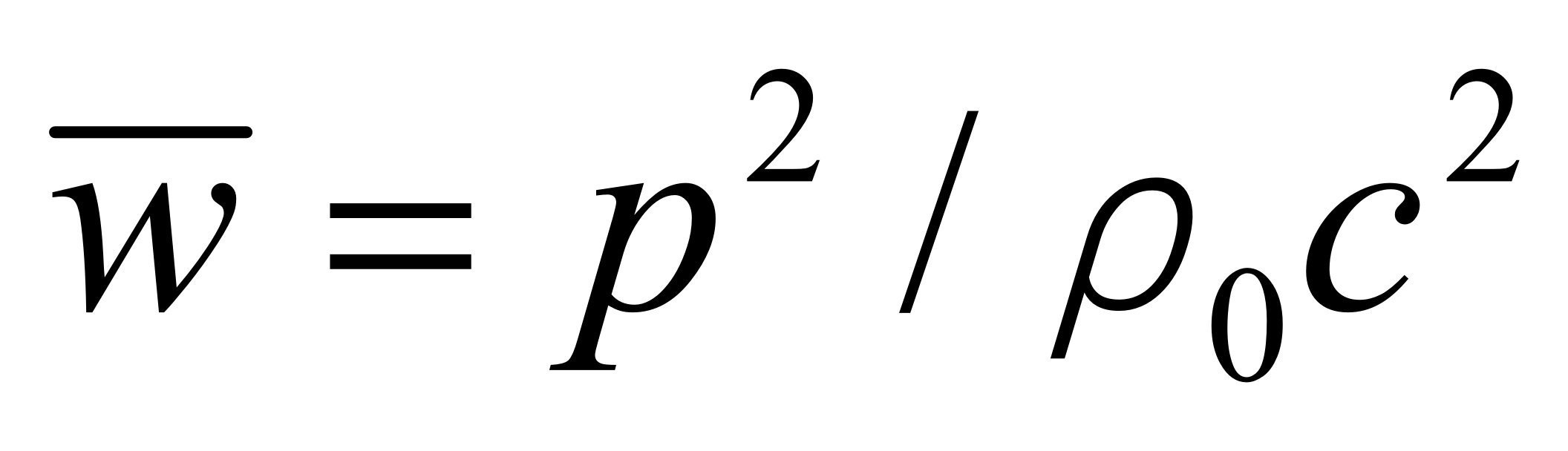= 2.81×10^-5 J/m³，它的辐射压力也是2.81×10^-5 N/m²。电磁波也具有相同的计算方法，例如场强为100dBmv的电磁波，其电场强度为100 v/m，可计算出它的平均能量密度为 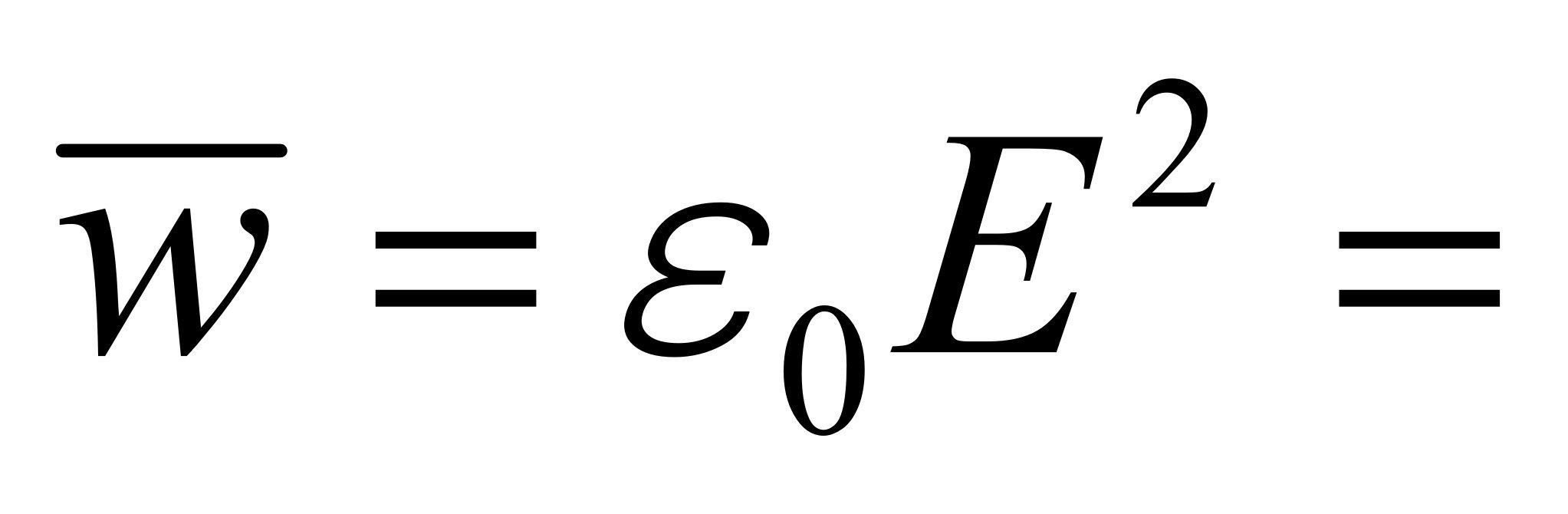8.85×10^-8 J/m³ ，它的辐射压力也是8.85×10^-8 N/m² 。

声波与电磁波的更大相同之处在于：当波完全反射时的辐射压力是完全吸收时的两倍。

• 波动方程

声波的波动方程可表示为：，，电磁波也具有相同的表示：，。

• 传播速度

声波在介质中的传播速度可表示为：，其中表示传播介质的体积压缩系数，它与体积弹性模量P的关系为：，电磁波的传播速度可表示为：。

• 传播特征

声波具有反射、折射、干涉、衍射、聚焦、多普勒效应等一系列的传播特征，电磁波也同样具有上述所有特征，声波中的有关定理在电磁波同样可用，而且计算方法也一样。更有甚者，波的指向角（衍射极限）都可以用表示，其中，λ是波长，D是波源的直径。总之，声波中的绝大部分特征在电磁波中都能找到与之相对应的项。从以上比较可以看出，声压p与电场强度E等价，体积元速度u与磁场强度H等价，介质密度与真空磁导率等价，体积压缩系数（）与真空介电常数等价。

2.1.2. 为什么声波与电磁波如此相似？

电磁波依靠电与磁的互激进行传播的理论是无法解释上述现象的（光子理论更无法解释），因为在电磁波中，E与H的关系是线性的，E和H也是同步变化的（相位相同）：

，E和H之间没有发生能量交换，E和H在空间的任何一点同时由小到大，再由大到小地变化，难道E和H在空间能够自生自灭？当E与H都是零时，电磁波的能量贮存在哪里？ 

如果承认以太的存在，那么，电磁波与声波的相似性就很容易理解，我们可以定义E就是以太受到粒子扰动后所产生的压强变化量，与声压p具有完全相同的物理意义，定义H是以太的体积元速度，其物理意义与声学中的体积元速度u相同。引入以太后，电磁波中的各种参数具有了明确的物理意义：真空磁导率就是以太的密度，真空介电常数就是以太的体积压缩系数，以太中的传播速度就是合情合理的。如果以太不存在，电磁波中的各种参数没有物理意义。

2.1.3. 定义的合理性

在电磁波中，把E定义为以太的压强变化量，把H定义为以太的体积元速度，与现代电磁理论具有本质的区别。也就是说，在电磁波中，我们所测量的电场强度实际上是以太压强的变化量，磁场强度是以太体积元的速度。

我们知道，所谓场强的测量，实际上是测量天线上感应的电压，天线上的电压是如何感应出来的成为关键，要想使天线上感应出电压，必须要有某种力量推动电子运动。

是什么力量推动的电子？学界主流认为是电场。如果是电场，那么，电场是什么就必须说清楚，在空无一物的真空中，是什么推动的电子？如果承认电场是物质，相当于变相承认了以太。如果承认以太的存在，就可以很明白地说明一切：电子是以太粒子推动的，电子的振动能产生电磁波，同样，电磁波也能使电子产生振动。

因此，E只是一个符号，它代表一个物理量，它是什么要根据假设和推理，我们对天线的测量，只能得到感生电压或电流，重要的是这个电压或电流是如何产生的，是空间中的什么物理量产生的它。如果你认为是电场，你就应该定义E为电场强度，如果你认为是以太的振动产生的，就应该定义E为以太的压强变化量，定义H也是同样的道理。我们在话筒的输出端测量到的也是感应电压，但产生这个感生电压的原因却是空气的振动，天线与话筒实质上都是传感器。本文中仍然用E代表以太的压强变化量，H代表以太体积元的速度。

2.1.4. 小结

以太的密度可表示为真空波阻抗与光速的商：= 1.257×10^-6 kg/m³，其值与电磁场中的真空磁导率相等。需要指出的是：真空磁导率在电磁场中，只是麦克斯方程中定义的一个常数，其作用是单位的变换，没有物理意义。

2.2. 以太的温度T

温度是表示物体冷热程度的物理量，微观上，是物体分子热运动的剧烈程度，在数值上（绝对温标）等于物体的分子或原子所具有的平均能量除以玻尔兹曼常数：，对于固体，指的是原子的振动能量，对于气体，指的是粒子的动能，如果粒子没有振动或运动，其温度为0 K。

2.2.1. 气体辐射的原因

以太充满宇宙的各个角落（包括原子的内部），任何粒子在以太中运动时都会产生振动，其振动频率为，这个振动在以太中的传播就是辐射。例如：假设一个氮分子在以太中的运动速度为300 m/s，则这个氮分子的能量为= 2.1×10^-21 J，它的辐射频率为= 6.35×10¹² Hz，它的温度为= 152.5 K。气体的辐射主要来自粒子在以太中运动中所产生的振动和气体分子碰撞所产生的韧致辐射，所辐射的频率是它的固有频率。

2.2.2. 空气的温度与辐射

空气主要是由氮和氧分子构成的，分子结构为对称型双原子气体（如O₂、N₂、H₂等），具有微弱的辐射和吸收能力，一般可认为属于热辐射的透明介质，虽然它们的辐射能力很弱，但它们的辐射频谱仍与黑体辐射谱相同。在标准状态下（0 ⁰C，1atm），根据麦克斯韦-波尔兹曼函数，可得空气分子的最可几速率= 394.5 m/s，均方根速率= 483 m/s。由于，可得粒子的平均振动频率为= 1.71×10¹³ Hz。空气的辐射基本遵从黑体辐射，光谱辐射的峰值符合维恩定律：= 2897/273.15 = 10.6μm（此时辐射的频率f_λ  = 2.83×10¹³ Hz），光谱辐射的峰值符合：= 1.61×10¹³ Hz。

2.2.3. 宇宙微波背景辐射

宇宙微波背景在黑体辐射光谱上的温度为2.72548±0.00057K。光谱辐射的峰值为160.2GHz，在微波中的毫米波频率的范围内（若光谱辐射的定义为，则峰值波长为1.063毫米），该光谱在所有方向中几乎一致，但细微的变化展现出各向异性。

如何解释这种现象在学界产生了巨大的分歧，主流认为，宇宙诞生于距今约137亿年前的一次“大爆炸”，宇宙微波背景辐射是“大爆炸”的“余烬”，均匀地分布于整个宇宙空间。但是，如果是“大爆炸”遗留下来的电磁波辐射，不可能是各向同性、理想的黑体辐射。

本文认为：任何物质只要温度大于绝对零度，都会有辐射，以太也不例外。观测表明：宇宙背景辐射的波谱堪称理想的黑体辐射，完全有理由相信宇宙背景辐射就是以太气体所产生的辐射。

2.2.4. 小结

地球附近以太的温度就是宇宙微波背景在黑体辐射光谱上的温度，其值为2.725 K。需要指出的是：与空气一样，以太在宇宙中的温度并不是恒定的，致密星体附近的以太温度高。

2.3. 以太的静态压强P₀

在任何理想气体中，气体的体积弹性模量可表示为（c是波在气体中的传播速度），以太也不例外，可以算出以太的体积弹性模量= 1.1294×10¹¹ Pa，而静态压强P₀与体积弹性模量P的关系为，其中γ是比热比。

比热比指的是定压比热Cp与定容比热Cv之比，也称为绝热指数。根据分子运动理论，γ的理论值为，其中n为气体分子微观运动自由度的数目。当原子气体分子只有三个平移运动自由度，即n=3，故γ=5/3。氩、氦等单原子气体的γ实验值(1.66)与此非常接近。双原子气体分子除有三个平动自由度外，还有两个转动自由度，即运动自由度n=5，所以γ=7/5。多原子分子如H₂O 、氨等，只要各原子不是直线排列的（CO₂的自由度为5，为直线型），就可以看成自由刚体，共有6个自由度，可见，比热比只与分子的自由度有关。

对于以太粒子，可以看成自由质点，所以有3个平动自由度，因此，可以认为以太的比热比γ= 5/3。根据以太的比热比，可以算出地球表面以太的静态压强 P₀= 6.78×10¹⁰ Pa，相当于67万个大气压。

是什么使以太的静态压强如此之大？包括银河系中心在内，都不可能具有这种能力，因此，可以推测：它是由巨引源（超星系团的重力中心）产生的。可以看出，连银河系这样的庞然大物，也不过是漂浮在以太大海中的一片树叶。

2.4. 以太粒子的质量m

 对于由理想气体组成的介质，介质的粒子质量可由计算出来。例如，对于空气介质，在标准状态下，取空气的比热比γ= 1.4，空气温度T= 273.15 K，传播速度c = 331.2 m/s，可计算出空气粒子的平均质量为m = 4.81×10^-26 kg。同理，已知以太的温度T = 2.725 K，传播速度c = 299792458 m/s，比热比γ= 5/3，可得出以太粒子的平均质量：m = 6.974×10^-40 kg。假设以太粒子是球形，而且密度为2×10¹⁸ kg/m³ ，可以计算出以太粒子的半径为4.37×10^-20 m。

2.5. 以太的气体常数R

对于普通理想气体物质，气体常数定义为1 mol的理想气体在可逆定压加热过程中温度每升高1K时对外所作出的膨胀功，其值为= 8.31 J/(mol.K)，（对于标准状态下的空气，大气压强P为101325 Pa，体积V为0.0224 m³，温度T为273.15K）。玻尔兹曼常数k表示气体升高1度，每个粒子对外所作出的膨胀功，其值为R除以所含的粒子个数（也就是阿伏加德罗常数N_A = 6.022×10²³），即:= 1.38×10^-23 J/K。根据摩尔的定义：1摩尔任何物质含有N= 6.02×10²³个微粒，由于以太的密度ρ= 1.257×10^-6 kg/m³，粒子质量m = 6.974×10^-40 kg，因此，1摩尔的以太质量为：= 4.2×10^-16 kg，1摩尔的以太体积为：= 3.34×10^-10 m³。以太的标准状态为：静态压强P₀ = 6.78×10¹⁰ Pa，温度T = 2.725 K，气体常数= 8.31 J/(mol.K)，与普通理想气体相同。

2.6. 以太与空气比较

以太与空气具有非常相似的物理性质，二者的比较如表2-1所示：

表2-1.以太与空气的比较

参数	空气(0˚C, 1 atm)	以太(T = 2.725 K)	关系
静态密度ρ0 (kg/m3)	1.29	1.257 × 10−6
静态压强P0 (Pa)	1.01 × 105	6.78 × 1010
比热比γ	1.40	1.67
传播速度c (m/s)	332	3.0 × 108
体积弹性模量P (Pa)	1.43 × 105	1.13 × 1011	=YP0
波阻抗Z(Ω)	427.6	376.7	=p0c
体积压缩系数β (Pa− 1)	7.0 × 10−6	8.85 × 10− 12	= 1/E
最大辐射处波长λ (m)	1.06 × 10−5	1.06 × 10−3	= b/T
粒子最可几速度vp (m/s)	395	3.28 × 108	=
粒子平均质量m (kg)	4.81 × 10−26	6.974 × 10−40	=ykT/c2
每立方米粒子个数N(m−3)	2.69 × 1025	1.8 × 1033	=p0/m
气体常数R（J/mol.K)	8.31	8.31	P0V/T
粒子平均平动动能E (J)	5.67 × 10−21	5.67 × 10−23	= 1.5kT

本文由奇点天文作者上传并发布，奇点天文仅提供文章投稿展示，文章仅代表作者个人观点，不代表奇点天文立场。